朱成秀 随岁寒 彭丹华 李成†
(1. 苏州大学 轨道交通学院,苏州 215131) (2. 商丘工学院 机械工程学院,商丘 476000)
轴向运动系统在实际工程中应用广泛,常见的例子有传动带、数控机床的进给系统、机器人末端执行器等[1, 2].为提高这些工程装备的工作效率,对轴向运动速度提出了要求.研究表明提高轴向运动速度能够降低固有振动频率[3],而对低频的振动控制通常是容易实现的.对于轴向运动系统,由于运动因素的存在,即使是低速情况下也会产生横向振动与轴向速度的耦合,从而影响系统的动态特性,导致系统模态的变化[4].因此,运动结构的横向振动往往是制约系统性能的重要原因,尤其是对高速精密系统而言.为了模拟和优化相关运动工程结构,运动系统的振动问题已成为近年来的研究热点[5-7].文献[8]建立了处于气动热环境下的热轧制造过程轴向运动板模型,考虑了运动速度、温度以及气流速度等因素对系统非线性振动的影响,为热轧工艺设计提供了参考.文献[9]基于基尔霍夫板理论,应用有限元方法,研究了流体中轴向运动板的振动问题,并考虑了速度与流体密度对板的振动稳定性的影响.文献[10]研究了流体中轴向运动梁的动力稳定性,其中考虑了流体附加质量以及非线性偏转轴向力的影响.文献[11]针对印刷设备中的运动薄膜,基于冯·卡门非线性理论,研究了运动薄膜的大变形振动问题.文献[12]基于薄板理论,利用哈密顿原理,研究了磁场中旋转运动圆板的分叉与混沌.
值得注意的是,上述研究均未涉及弹性支承对轴向运动结构的影响.在某些工程中,弹性支承是不可或缺的,其对系统横向振动的影响无法忽略.对于弹性支承-轴向运动系统,以往也有一些研究,但大多数都是一维弦或梁模型.文献[13]考虑了在弹性基础上的轴向运动梁模型的振动,研究了路径曲率、轴向速度以及支承刚度对固有频率的影响.文献[14]研究了外部激励下两端带有弹簧支承的轴向运动梁的固有模态.文献[15]应用铁木辛柯梁理论,研究了具有中间弹簧支承的轴向运动梁的非线性振动.文献[16]研究了具有中间弹簧支承的轴向运动梁在分布谐波激励下的纵向和横向非线性耦合振动和稳定性.文献[17]分析了由离散式弹性基础支承的轴向运动弦的临界速度与不稳定性.考虑弹性支承的轴向运动板的文献较少,文献[18]利用经典板理论研究了弹性支承下运动正交各向异性板的稳定性,文献[19]基于一阶剪切变形理论,研究了弹性基础支承的轴向运动双层板的动力响应.目前尚未见基于高阶剪切变形理论的轴向运动板-弹簧系统的研究.
为了更好地分析厚板的力学性能,研究人员发展了很多高阶剪切变形理论[20, 21].其中Reddy提出的三阶剪切变形理论认为横向剪切应变沿板厚呈抛物线分布[22, 23],能够比较准确地反映剪切板的变形与位移,并且计算量较小,已得到广泛应用[24, 25].文献[26]基于Reddy三阶剪切变形理论,研究了位于黏弹性介质上的碳纳米管增强功能梯度板的自由振动,并与一阶剪切变形理论结果对比揭示其优越性.文献[27]应用Reddy三阶剪切变形理论,分析了压电功能梯度板的弯曲与动力特性.
对于轴向运动板的有限元模型,以往多基于薄板理论,并应用哈密顿原理来推导方程,导致对于中厚板的振动预测存在一定误差[3, 9].本文基于三阶剪切变形理论,并应用虚功原理得到有限元方程,考虑了横向剪切应变沿板厚的分布情况,也能够适应于中厚板的振动分析,并且计算量相对于其他高阶变形理论较小.另外,工程结构常置于弹性基础之上,在多数情况下弹性基础可以看作分布式或离散式的弹簧支承.本文将离散式弹簧这一约束通过势能方程引入有限元模型中,并通过改变支承刚度矩阵中非零值的位置,调整离散弹簧支承作用在板面的位置,简化了模型的计算复杂度并提高了预测精确性.
综上,本文应用Reddy三阶剪切变形理论,研究弹性支承下轴向运动板的自由振动.将离散式弹簧支承引至势能方程,并采用一种四节点四边形单元离散板域,得到轴向运动板自由振动的有限元方程.在数值算例部分,利用ANSYS软件对静止板进行了前三阶模态分析,并将本文数值结果与ANSYS结果进行对比,证明本文方法的有效性.随后,探讨轴向速度、弹簧刚度以及板厚对弹性支承下轴向运动板的振动及其稳定性的影响.研究结果可为由空气轴承、张紧臂等支承的二维运动系统的设计与优化提供理论基础.
建立图1所示的矩形板模型,长、宽、高分别为a、b、h,沿x轴方向的运动速度为v.板的弹性模量为E,密度为ρ,泊松比为μ.板承受离散线弹簧支承,其刚度为k,不考虑转角刚度.

图1 受离散弹簧支承的轴向运动板Fig.1 Axially moving plate with discrete elastic supports
根据Reddy三阶剪切变形理论[22, 23],板的位移可由三阶多项式表示如下:
w(x,y,z)=w
(1)

由此可以得到应变分量与位移分量的关系:
(2)

为了离散求解域,采用四节点四边形单元,广义坐标如下:
(3)
其中
w=N{d}
φx=P{d}
φy=Q{d}
(4)
其中N、P、Q为形函数[28, 29],单元每个节点有横向挠度、绕x方向的转角、绕y方向的转角等3个自由度.
将式(3)和式(4)代入几何方程(2),并将其整理成矩阵形式:
ε=[B]{d}
(5)
其中
考虑应力应变关系,板的物理方程可以写成:
(6)
亦可将其表达为σ=[D]ε.
考虑式(5)与式(6),板的应变能变分如下:
(7)
将式(1)和式(4)代入可以得到惯性力做功的变分表达式:
(8)
由于板存在轴向运动速度,其科氏力和离心力做功的变分可表达为:
(9)
将式(7)、式(8)和式(9)代入如下虚功原理表达式:
δU=δW+δF
(10)
从而得输流管道系统的有限元平衡方程

(11)
其中
当板面上一点受到弹簧支承时,弹性势能变分为:
δUs={d}Tdiag(ann){d}
(12)
其中,ann为支承刚度矩阵对角线上唯一的非零值,下标代表第n行第n列,且ann=k.划分单元时将单元节点与弹簧支承点重合,从而该节点的横向位移对应的整体节点编号即为n.考虑支承刚度后系统的整体刚度矩阵为:
D=K+diag(ann)
(13)
将式(11)的Κ替换为D,得到受弹簧支承条件下轴向运动板自由振动的有限元方程:

(14)
考虑两种边界条件:四边固支、与运动方向垂直的两边固支另两边自由,板的材料参数与几何参数如表1所示.
为了验证本文提出的轴向运动弹性支承板模型及其结果的有效性,令板的速度为0,将弹簧刚度分别取极大值与极小值来模拟经典支承条件,然后进行模态分析,并将数值结果与ANSYS计算结果进行对比.

表1 数值算例中的参数值Table 1 Parameter values in numerical examples
在四边固支边界下,取板厚为0.02m,弹簧刚度为0,模拟无支承情况,弹簧刚度取正无穷时模拟刚性支承情况.图2为应用ANSYS有限元软件计算得到的模态图,其中图2(a)、(c)、(d)、(e)表示无支承板的前三阶模态,图2(b)为支承刚度无限大条件下的第一阶模态,第二阶模态分两部分,在速度为零的情况下,二者对应的固有频率相等,这与文献[30]和文献[31]的结论一致.对于无支承情况,随着振动模态阶数的提高,板的变形趋势不同,模态愈加复杂.其中无支承板的第一阶模态主要表现为板中心处的大变形,而刚性支承板的第一阶模态的最大变形量位于绕板中心的环状区域,板中心处的变形量等于0.值得注意的是,弹簧刚度为0的条件下,第二和第三阶模态的几何中心处横向变形为0.因此可以推断,当弹簧支承在该点时,弹簧刚度的变化对第二阶和第三阶没有影响.
图3为两边固定两边自由边界条件下板的前三阶模态.在刚度为0和无穷大两种情况下,最大变形量均位于自由板边的中点附近.在无弹性支承条件下,不同模态阶数下板的变形趋势不同.与四边固支不同的是,第三阶模态中板的几何中心处存在较大变形量,因此推断在两边固支两边自由边界约束下,当弹性支承在几何中心点时,弹簧刚度的变化仅对第二阶固有频率不产生影响.图3(b)表示在刚性支承条件下板的第一阶模态,与图3(a)对比可以看出,不同刚度下板的变形趋势存在较大差异,即刚度对板的模态影响较大.

(a) Mode 1 (k=0)
表2给出了弹簧刚度取0时,厚度分别为0.02m和0.2m的四边固支无运动板的前三阶固有频率,并将本文结果与ANSYS结果进行了对比.可见本文数值解与有限元解基本吻合,最大误差不超过3.97%,证明了本文模型的有效性.另外,本文结果相对于ANSYS结果固有阶频率均偏大,这是由于本文所采用的单元每个节点只有3个自由度,造成本文结果相比ANSYS结果偏大.由于本文基于三阶剪切变形理论,因而对厚板也有良好的适用性,这一点也可由表2中厚度0.2m的对比结果佐证.表3为厚度为0.02m的无运动板在两边固支两边自由边界条件下的前三阶固有频率与ANSYS对比结果,同样具有较好的一致性,证明了本文模型在不同边界条件与不同刚度下均可以取得理想的结果.
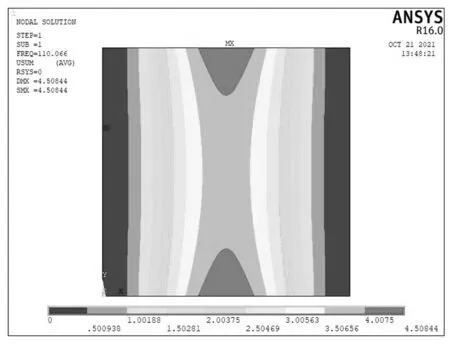
(a) Mode 1 (k=0)

表2 四边固支无运动板的前三阶固有频率(k=0,v=0)Table 2 The natural frequencies of a stationary plate fixed at four edges
为了分析弹簧刚度与运动速度对模型稳定性的影响,作为对比,图4描述了四边固支条件下,弹簧刚度为0即无支承情况下轴向运动板前三阶固有频率随速度的变化.在速度为0时,前三阶频率实部均为0,随着速度增加,固有频率的虚部逐渐降低,这表明速度的增加使板的刚度降低.当速度增加到320m/s,第一阶固有频率的虚部减小到0,实部由0变为两个分支,此时速度为第一阶模态速度的发散临界值,在临界值到达前,轴向运动板始终保持稳定.在320~340m/s的速度区间内,第一阶振动模态不稳定,固有频率保持实数形式.当速度增加到350m/s时,第一阶固有频率实部回归到0,并且虚部呈上升趋势.第二阶振动模态中包含的两个固有频率在速度较小时保持相等,随着速度增加,二者逐渐分离.另外,第二和第三阶固有频率在0~390m/s区间内保持实部为0,模型在第三阶模态始终具有稳定性.

表3 两边固支两边自由无运动板的前三阶固有频率Table 3 The natural frequencies of a stationary plate fixed on two opposite edges and the others free

(a)实部(a) The real part
令弹簧刚度k=40×106N/m,图5为弹性支承下四边固支轴向运动板随速度的变化.与图4类似,在速度较小时,前三阶固有频率实部均为0且虚部随速度增大而降低,板保持稳定状态.第一阶固有频率的值在相同速度下大于无支承时的情况,这表明弹性支承有效增加了板的刚度.第一阶模态的速度临界值为350m/s,相比无支承时变大,在350~400m/s区间内,第一阶固有频率为不稳定状态,不稳定区间的长度相比无支承时增加.第二阶模态包含的两个固有频率分离时的速度相对于无支承时变小,但在速度较大时二者又回到几乎相等的状态.另外,在0~400m/s区间内,第二、三阶固有频率实部始终为0,板在第二、三阶模态保持稳定.第二和第三阶固有频率与弹簧刚度为0时相同,从而验证了前文预测.由此可推知,根据振动控制的需要,可以通过采用不同的弹簧布置方式来控制特定模态的振动.
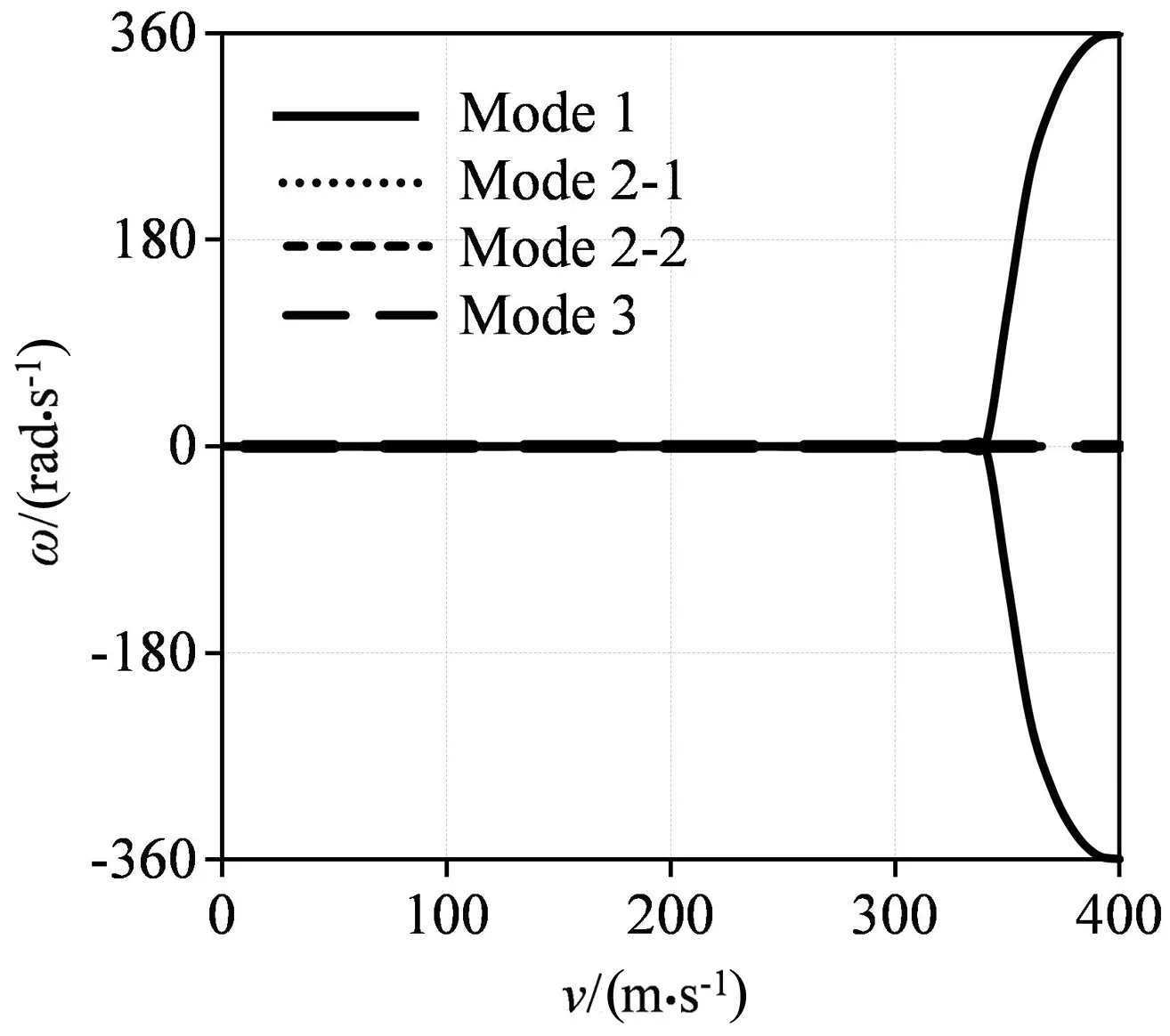
(a)实部(a) The real part
令弹簧刚度趋于无穷大,由于仅仅限制了弹簧位移,截面转角仍保持自由状态,经本文算法验证,离散点刚性支承等价于该点简支的情况.图6给出了局部简支支承下轴向运动板的前三阶固有频率与速度的关系.在速度较小时,板的前三阶频率仍然保持实部为0,且虚部随着速度增大而减小.但在0~400m/s的速度区间内,前三阶固有频率不再出现发散情况,轴向运动板始终保持稳定,这一点与无支承及弹性支承时存在显著差异.另外,第二阶模态的两个固有频率分离时的速度大幅减小,几乎在速度为0时就分离,并且分离程度更加显著.局部简支支承板的第一阶固有频率在相同速度下均大于弹性支承情况,这证实了弹簧刚度增大能够有效增加板的刚度.但值得注意的是,第二、三阶固有频率几乎没有变化,进一步验证了基于模态的预测.另外与图4和图5不同,离散点简支时轴向运动板的第一阶固有频率大于第二阶,这是由于弹簧刚度对第一阶频率的影响远大于第二、三阶,使得第一阶模态发生了扭曲(如图2(b)),从而造成了第一阶固有频率超越无支承条件下的第二阶情形.

(a)实部(a) The real part
图7分析了弹簧刚度对两边固支两边自由板固有频率的影响,与四边固支时相似,在不同弹簧刚度下,前三阶固有频率均随速度增加而降低,证明了轴向运动速度的增加会降低板的总体刚度.由图7(a)可以看出,在弹簧刚度为0时,板的一阶速度发散临界值约为200m/s,远低于四边固支边界情形.由图7(b)可见,随着速度增加,一阶固有频率与二阶固有频率逐渐趋于重合,这表明板的一阶与二阶固有频率可能出现耦合,板将发生颤振不稳定现象.另外,在不同弹簧刚度下,第二阶固有频率没有发生变化,证明了前文模态分析时的推断.注意到与四边固支的情况类似,弹簧刚度对第一阶固有频率的影响大于第二阶,从而使第一阶模态扭曲[如图3(b)],导致了图7(c)中第一阶固有频率超越了第二阶.
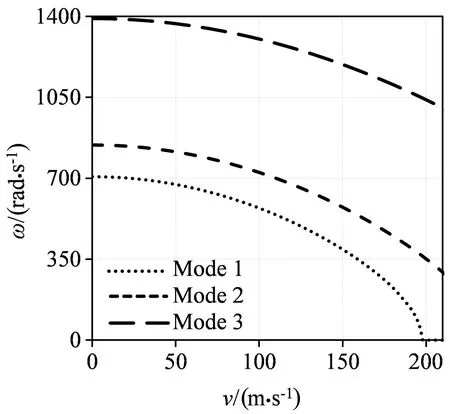
(a) k=0×106 N/m
下面考虑板厚的影响,为了进行对比,取板厚h=0.2m,考虑四边固支无支承时的轴向运动板,其前三阶固有频率的虚部随速度变化如图8所示.与图4结论一致,随着速度增加,固有频率呈现下降趋势.相比于图4,前三阶固有频率大幅增加,这表明增加板厚可以显著提高轴向运动板的刚度.另外,模型在图示速度区间始保持稳定,可推知第一阶模态的速度临界值远大于板厚为0.02m的薄板,这说明较厚的板在高速下能保持稳定.
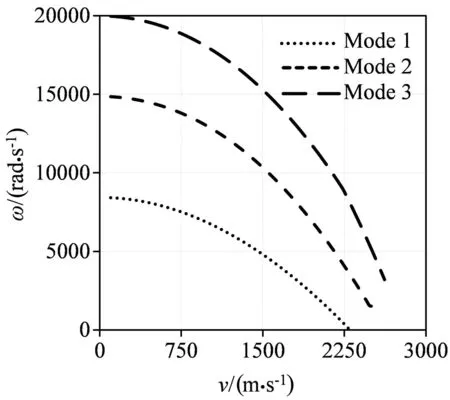
图8 四边固支弹性支承轴向运动板前三阶固有频率 (h=0.2m, k=0×106 N/m)Fig.8 The complex frequencies of the elastically supported axially moving plate fixed at four edges (h=0.2m, k=0×106 N/m)
基于Reddy三阶剪切变形理论研究了弹簧支承下轴向运动板的自由振动,应用四节点四边形单元进行有限元建模和求解,其中考虑了离散式弹性支承与轴向速度,并通过系统势能的形式直接将弹簧支承条件考虑到有限元方程中,从而求得板的动力稳定性.主要结论如下:
1) 运动速度的增加会降低轴向运动板的总体刚度,当速度增加到发散临界值时,板在一定速度区间内会出现不稳定现象.在两边固支两边自由边界条件下,第一阶与第二阶固有频率会发生耦合,从而导致板出现颤振不稳定.
2) 弹簧刚度增大能有效增强轴向运动板的刚度,并提高振动固有频率,且速度发散临界值随着弹簧刚度的增加而提高.另外,当弹簧在中心点支承时,在四边固支条件下,弹簧刚度对第一阶固有频率影响较大,而对第二和第三阶基本无影响.在两边固定两边自由边界下,弹簧刚度仅对第二阶固有频率影响较小.因此可通过改变弹簧布置方式来控制特定模态的振动.
3) 当板厚变大时,固有频率与速度发散临界值均得以显著提高,证明了厚板具有更高的刚度与更好的振动稳定性.
猜你喜欢固支三阶固有频率三阶非线性微分方程周期解的非退化和存在唯一性数学物理学报(2022年2期)2022-04-26翅片管固有频率的参数化分析及模拟研究化工机械(2022年1期)2022-03-21不同边界条件薄壁截锥壳的高阶振动特性研究辽宁科技大学学报(2021年4期)2021-11-26一角点支撑对面两边固支正交各向异性矩形薄板弯曲问题的辛叠加解应用数学(2020年3期)2020-07-28新型三阶TVD限制器性能分析北京航空航天大学学报(2017年4期)2017-11-23巧填三阶幻方中学生数理化·七年级数学人教版(2017年2期)2017-03-25总温总压测头模态振型变化规律研究现代机械(2015年1期)2015-01-15三阶微分方程理论国外科技新书评介(2014年12期)2015-01-05A novel functional electrical stimulation-control system for restoring motor function of post-stroke hemiplegic patients中国神经再生研究(英文版)(2014年23期)2014-06-01转向系统固有频率设计研究客车技术与研究(2014年3期)2014-03-20